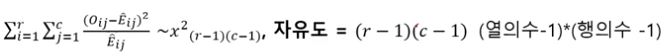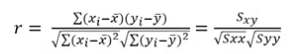JinWoo Kim

백문이 불여일견, 백견이 불여일행.

2 minute read

통계 - 개념 정리

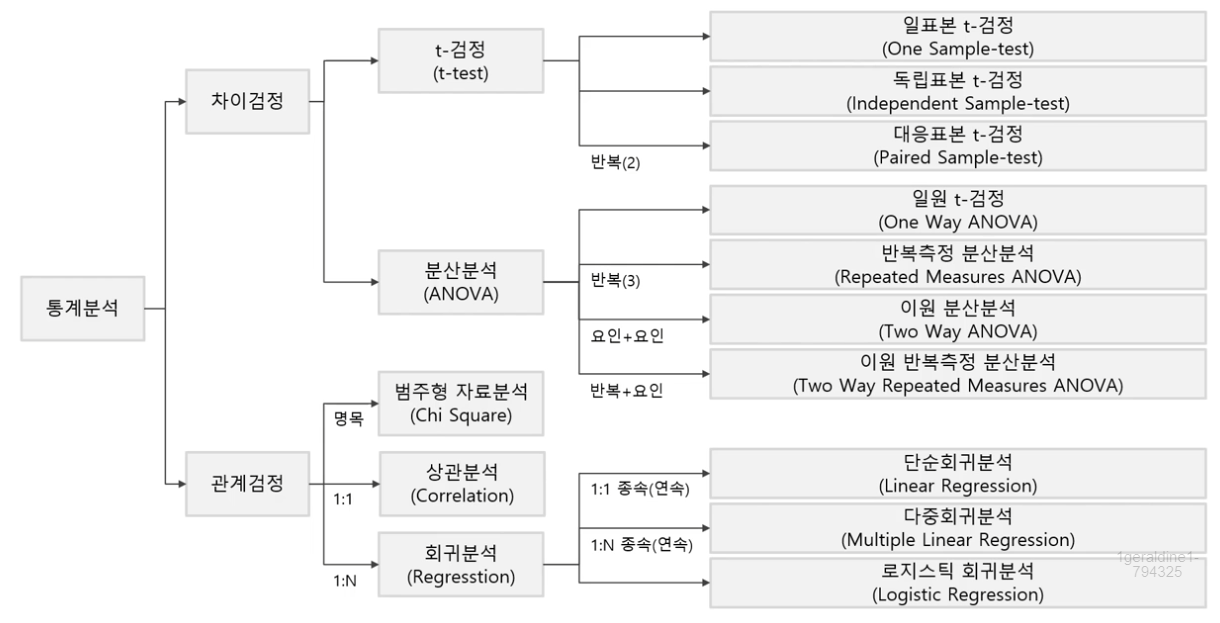
가설검정과 유의수준

가설 검정

  • 가설 + 검정

  • 가설 : 주어진 사실 또는 조사하려고 하는 사실에 대한 주장 또는 추측을 가설이라고 함

  • 통계학에서는 특히 모수를 추정할때 모수가 어떠하다는 증명하고싶은 추측이나 주장을 가설이라 함

귀무가설(Null hypothesis: $H_0$)

  • 기존의 사실

  • 대립가설과 반대되는 가설
  • 연구하고자 하는 가설의 반대 가설
  • 귀무가설은 연구목적이 아님

대립가설(Alternative hypothesis: $H_1$)

  • 데이터로부터 나온 주장하고 싶은 가설 또는 연구의 목적

  • 귀무가설의 반대

제1종 오류

  • 귀무가설은 참이지만, 귀무가설을 기각하는 오류

  • $H_0$를 기각할 확률이 $a$라고 하면 채택하게될 확률은 $1-a$로 표시할수 있음.

  • 제1종 오류를 범할 확률의 최대허용 한계를 유의수준이라 하며, $a$라고 표시

제2종 오류

  • 귀무가설이 기각해야 하지만, 귀무가설을 채택하는 오류

검정통계량

  • 귀무가설이 참이라는 가정하에 얻은 통계량

  • 검정결과 대립가설을 선택하게 되면 귀무가설을 기각함

  • 검정결과 귀무가설을 선택하게되면 귀무가설을 기각하지 못한다고 표현함

p-value

  • 귀무가설이 참일 확률

  • 0~1 사이의 표준화된 지표(확률값)

  • 귀무가설이 참이라는 가정하에 통계량이 귀무가설을 얼마나 지지하는지를 나타낼 확률

기각역(reject region)

  • 귀무가설을 기각시키는 검정통계량의 관측값의 영역

가설검정의 절차

  1. 가설 수립
  2. 유의 수준 결정
  3. 기각역 설정
  4. 검정통계량 계산
  5. 의사 결정

양측 검정(two-side test)

  • 대립가설의 내용이 같지 않다 또는 차이가 있다 등의 양쪽 방향의 주장

단측 검정(one-side test)

  • 한쪽만 검증하는 방식
  • 대립가설의 내용이 크다 또는 작다 처럼 한쪽 방향의 주장

단일 표본에 대한 가설검정

모평균 가설검정

모분산을 아는 경우 - Z 검정

  • 정규분포 사용

  • 검정통계량 : $z = \frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}} \sim N(0,1)$

  • 기각역 : $z_0 = \frac{\overline{X}-\mu_0}{\sigma/n}$

모분산을 모르는 경우(소표본) - T 검정

  • T분포 사용

  • 검정통계량 : $T = \frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}} \sim t(n-1)$

  • 기각역 : $t_0 = \frac{\overline{X}-\mu_0}{\sigma/n}$

모비율 가설검정

  • 정규분산 사용

  • 검정통계량 : $z = \frac{\hat{p}-p}{\sqrt{p(1-p)/n}} \sim N(0,1)$

  • 검정통계량 관측값 : $z_0 = \frac{\hat{p}-p_0}{\sqrt{p_0(1-p_0)/n}} \sim N(0,1)$

두개의 표본에 대한 가설 검정

대표본 - 모분산을 아는 경우

  • 검정통계량 : $z = \frac{(\overline{X_1}-\overline{X_2})-(\mu_1-\mu_2)}{\sqrt{\sigma_1^2/n_1 + \sigma_2^2/n_2}} ~ N(0,1)$

  • 검정통계량 관측값 : $z_0 = \frac{(\overline{X_1}-\overline{X_2})}{\sqrt{\sigma_1^2/n_1 + \sigma_2^2/n_2}}$

소표본 - 모분산을 모르는 경우

  • T분포 사용

  • 검정통계량 : $T = \frac{(\overline{X_1}-\overline{X_2})-(\mu_1-\mu_2)}{S_p\sqrt{1/n_1+1/n_2}} \sim t(n_1+n_2-2)$

  • 검정통계량 관측값 : $T = \frac{(\overline{X_1}-\overline{X_2})}{S_p\sqrt{1/n_1+1/n_2}}$

대응 비교

  • 쌍으로 조사된 자료가 주어졌을때 $X_i$의 평균을 $\mu_x$, $Y_i$의 평균을 $\mu_y$라고 하면, $D_i=X_i-Y_i$로 정의함.

  • 검정통계량 = $T = \frac{D-\mu_D}{S_D\sqrt{n}} \sim t(n-1)$

  • 검정통계량 관측값 : $T_0 = \frac{D-\mu_D}{S_D\sqrt{n}}$

정리

  • 가설검정에서
    • 대표본일때 : Z분포 사용
    • 소표본일때
      • $\sigma^2$를 안다 : Z분포 사용
      • $\sigma^2$를 모른다 : T분포 사용

범주형 자료분석

  • 범주형 자료
    • 관측된 결과를 어떤 속성에 따라 몇개의 범주로 분류시켜 도수로 주어진 데이터
  • 범주형 자료분석
    • 범주형 자료에 대한 통계적 추론 방법
    • 범주형 자료분석은 카이제곱 검정으로 추론함

T-test와 카이제곱 검정의 차이

  • T-test : 연속형 변수의 차이에 대한 검정
  • 명목형 변수에 대한 검정시 카이제곱 검정을 사용

적합도 검정

  • 관측된 값들이 추론하는 분포를 따르고 있는지 검정

  • 한개의 요인을 대상으로 검정

검정 방법

  • $\chi^2= \Sigma{\frac{(O_i-E_i)^2}{E_i}}$, 자유도 = 범주의 개수 - 1

    • O는 관찰 빈도 : 데이터로부터 수집된 값

    • E는 기대 빈도 : 기대값과 비슷한 개념

독립성 검정

  • 관측된 값을 두개의 요인으로 분할하고 각 요인이 다른 요인에 영향을 끼치는지(독립성)를 검정

검정 방법

동질성 검정

  • 서로 다른 세개 이상의 모집단으로 관측된 값들이 범주내에서 동일한 비율을 나타내는지 검정

범주형 분석을 어떻게 해야하는가?

  • 엑셀의 pivot기능을 많이 쓴다.
    • 즉, 범주형 데이터를 많이 다룬다.
  • 시간의 흐름에 따라서 어떤 산업이 거래액이 증가하고 있는가?
    • 시간의 흐름에 따른 데이터 변화
  • 어떤 업종이 비중이 떨어지는가?
    • 데이터의 비중 변화

  • 통계적 개념이란 결국, 논리적인 사고를 펼쳐나가다가 근거에 대한 수치를 구해야할때 사용하는것.

  • 비즈니스 인사이트와 통계적 분석을 때에 따라 적절히 활용하는것이 중요.

상관분석

상관관계

  • 두 변수간의 함수관계가 선형적인 관계가 있는지 파악할 수 있는 측도가 상관계수.

  • $\rho = Corr(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)}\sqrt{Var(Y)}}$

  • 상관계수의 특성

    1. 상관계수는 $ -1 \le \rho \le 1$
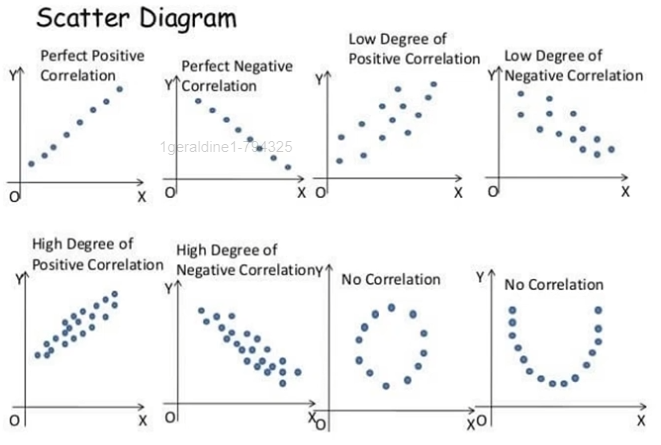
    2. 상관계수가 1에 가까울수록 양의 상관관계가 강함
    3. 상관계수가 -1에 가까울수록 음의 상관관계가 강함
    4. 상관계수가 0에 가까울수록 두 변수간의 상관관계가 존재하지 않음
    5. 상관계수가 0이라는것은 두 변수간에 선형관계가 존재하지 않는다는것.

표본 상관관계

  • 데이터가 쌍으로 주어졌을때,

  • 가설 검정

    1. 가설 수립 $H_0: \rho = 0 \quad vs \quad H_1: \rho \neq0$

    2. 검정통계량 : $T=\sqrt{n-2}\frac{r}{\sqrt{1-r^2}}$

  • 점그래프로 보는 상관관계

You May Also Enjoy