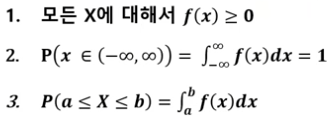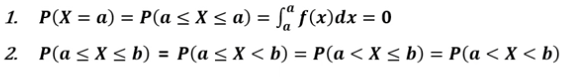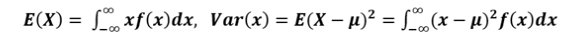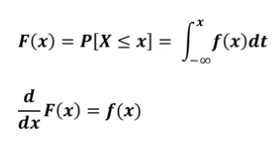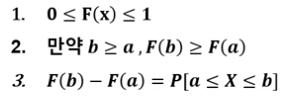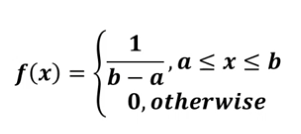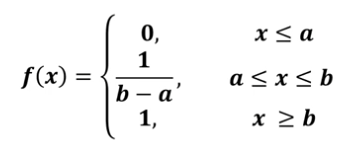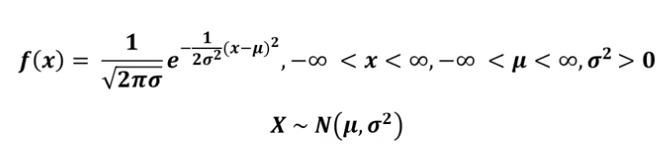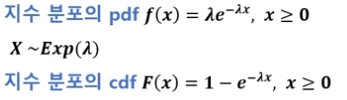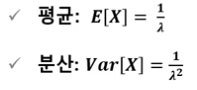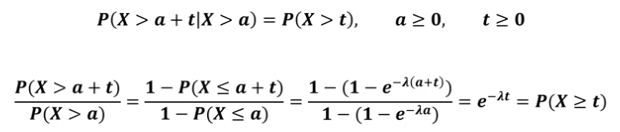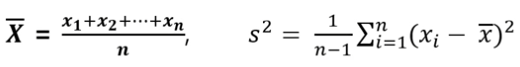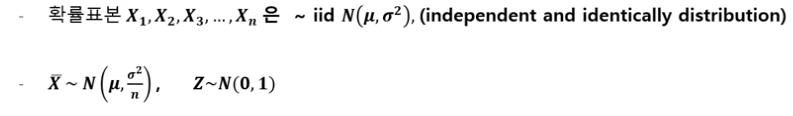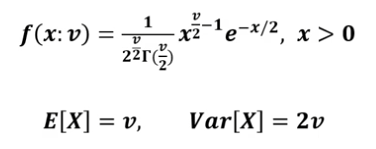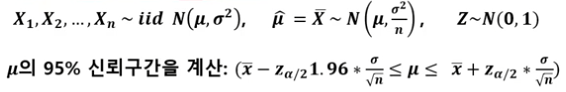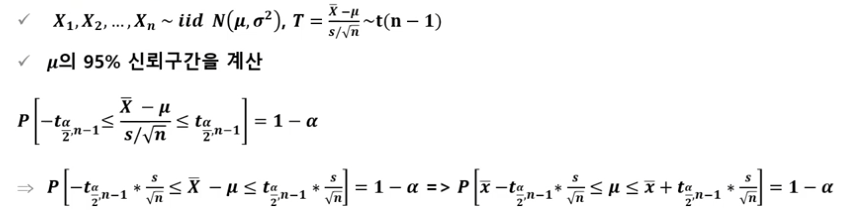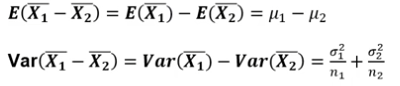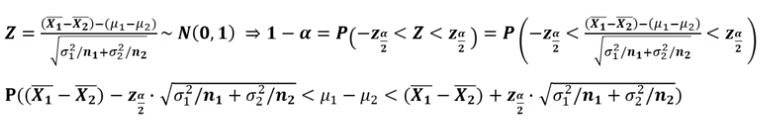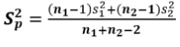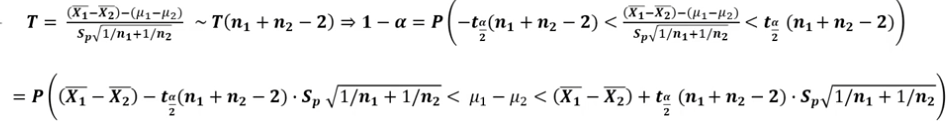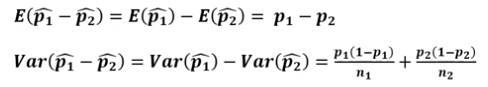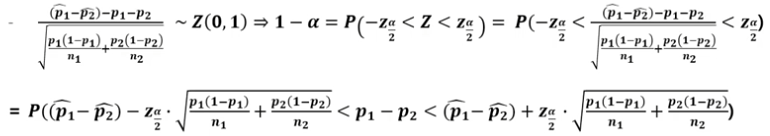JinWoo Kim

백문이 불여일견, 백견이 불여일행.

4 minute read

통계 - 개념 정리

연속형 확률 분포

확률 밀도 함수(pdf)

  • 연속형 확률 변수 X에 대해서 함수 f(x)가 아래의 조건을 만족하면 확률밀도함수라고 함.

  • 확률밀도함수의 성질

  • 확률밀도함수의 평균과 분산

누적분포함수(cdf)

  • 확률밀도함수를 적분하면 누적분포함수가 됨

  • 누적분포함수의 성질

균일 분포

  • 모든 확률변수에 대해 균일한 확률을 갖는다.

  • 확률변수 X가 폐구간[a,b]내의 모든 영역에서 일정한 확률을 가질 때, 이 확률변수 X를 균일확률변수라고 한다.

  • 폐구간 [a,b]내의 모든 구간에서 일정한 크기의 확률을 가질 때, 균일확률변수 X의 확률밀도함수 f(x)는 다음과 같다.

  • 균일분포의 누적분포함수는 다음과 같다.

정규 분포

  • 가우스 분포 라고도 불림.

  • 확률밀도함수는 확률변수X가 평균이 μ이고 분산이 σ2인 정규분포를 따를때 아래와 같다.

  • 정규분포의 특성

    • 중심인 μ를 기준으로 좌우대칭
    • 중심인 μ에서 가장 높은 확률을 가짐
    • 그래프 면적의 합이 1

  • 정규분포의 평균과 분산

    • 평균 : E[X] = μ
    • 분산 : Var[X] = σ2
    • 표준편차 : σ

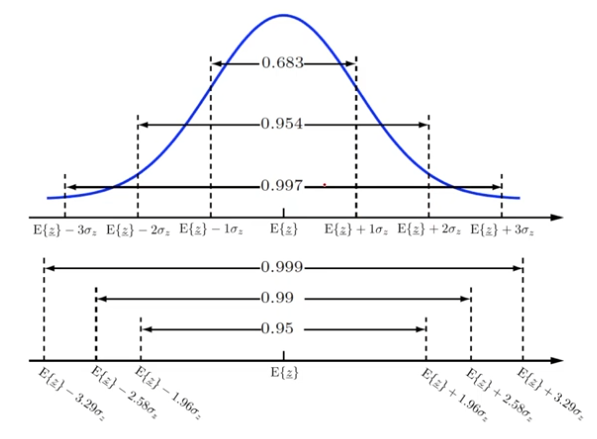
  • 정규 분포의 성질

  • 이항 분포의 정규 근사

    • X ~ B(n,p)일때, 확률변수 X는 n이 충분히 크면 근사적으로 정규분포 X ~ N(np,np(1-p))를 따른다.

표준 정규 분포

  • 확률변수 $X$ ~ $N(μ,σ^2)$정규분포를 따르고 확률변수 $z = (X-μ)/σ$라고 할때 확률변수는 Z~N(0,1)이다.

지수 분포

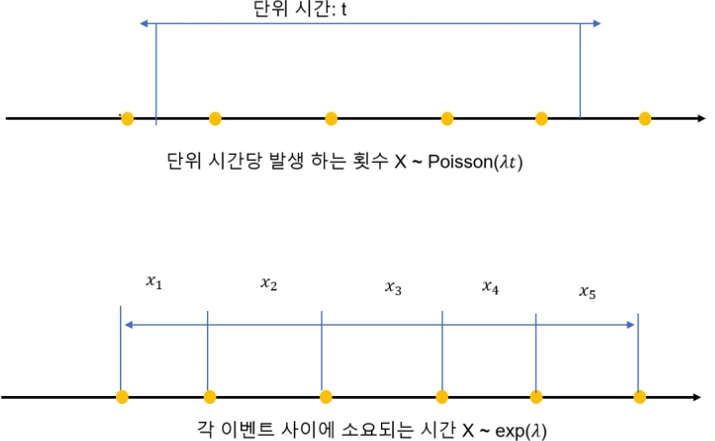
  • 단위 시간당 발생할 확률 λ인 어떤 사건의 횟수가 포아송 분포를 따른다면, 어떤 사건이 처음 발생할때까지 걸린 시간확률변수 X는 지수분포이다.

  • 지수 분포는 연속되는 사건 사이의 대기 시간도 지수분포이다.

  • 지수 분포의 평균과 분산

  • 지수분포의 무기억성

    • 어떤 시점부터 소요되는 시간은 과거 시간에 영향을 받지 않음

    • 지수분포로 계산했을때, 전구를 한달동안 사용했을때 남은 수명은 한달간 사용했던 영향을 받지 않음.

    • 이러한 문제로 인해 실제 적용에 문제가 있고, 생존 분석에서는 Weibull분포 또는 log-normal분포를 사용함.

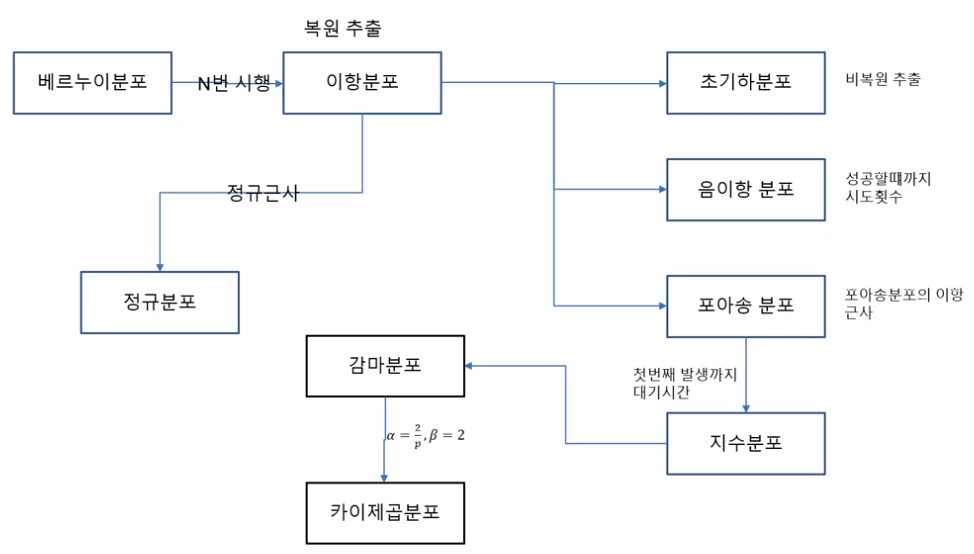
  • 지수분포와 포아송 분포의 관계

확률 분포의 관계도

모집단과 표본 분포

표본 추출(Sampling)

  • 모집단으로부터 표본을 추출하는것.
  • 표본으로부터 그 특성을 찾아내고, 모집단의 특성을 추론

표본 추출의 방법

  • 복원 추출
    • 모집단에서 데이터를 추출할때 하나를 추출하고 다시 넣고 추출하는 방식
    • 동일한 표본이 추출될수 있음
  • 비복원 추출
    • 모집단에서 데이터를 추출할때 하나를 추출하고 다시 넣지 않음.
  • Random Sampling
    • 모집단에서 데이터를 추출할때 주의할 점은 편향되지 않아야 한다는것.
    • 각 개체를 모두 동일한 확률로 추출하는 방법

불균형 데이터의 문제

  • 데이터가 불균형 데이터일 경우 문제가 생김.

  • 예측모형을 만드는 목적은 관심 대상이 발생할 확률을 예측하는것.
    • 예측 대상이 전체 대비 아주 낮을 경우, 모형의 성능에 대한 신뢰성 의문.
  • 해결 방법은 다음과 같다.
    1. Sampling 기법을 통하여 해결
    2. 모델을 통한 성능 개선(ex. Cost-sensitive learning)

Sampling 기법

  • 관심 대상의 비율이 아주 낮을경우 사용됨

  • Over Sampling
    • 타겟 데이터가 적은 class의 수를 많은 class의 비율만큼 증가시킨다.
    • 일정 비율로 복원추출하는 개념
    • 단, 과도적합의 문제가 발생할수 있다.
  • Under sampling

    • 타겟 데이터의 많은 class의 수를 적은 class의 비율만큼 감소시킴

    • 임의로 뽑은 데이터가 편향(biased)될수 있고, 모형의 성능이 떨어질수 있음.

통계량

  • 표본에 기초하여 계산되는 수치 함수

  • 표본 분포 : 통계량들이 이루는 분포

  • 표본평균 $\overline{X}$의 기대값은 $\mu$

  • 표본평균 $\overline{X}$의 분산은 $\frac{\sigma^2}{n}$

표본 분포

  • 모집단의 분포가 $N(\mu,\sigma^2)$이라고 할때, 다음과 같다

중심 극한 정리

  • 평균이 $\mu$이고 $\sigma^2$인 임의의 모집단에서 랜덤표본 $X_1,X_2 \dots X_n$을 추출할때
  • 표본의 크기 n이 충분히 ($n \geq 30$) 크면,
  • 표본평균 $\overline{X}$는 근사적으로 정규분포 $N(\mu,\sigma^2/n)$을 따른다.

카이제곱 분포

  • 확률변수 $Z_1^2, Z_2^2, \dots , Z_n^2$가 표준 정규 분포를 따른다면
    • 확률변수 $Z$는 $Z_1^2+Z_2^2+\dots+ Z_n^2$

  • $Z \sim \chi^2(v),Z$가 카이제곱 분포를 따를때

  • 카이제곱 분포는 감마 분포에서 $a=\frac{v}{2}, \lambda=2$와 같음

  • 카이제곱 분포는 범주형 자료 분석에서 활용함

카이제곱분포의 자유도

  • 자유도
    • 표본수-제약조건의 수 또는 표본수-추정해야하는 모수의 수를 의미하며, 일반적으로 n-1을 사용함.
  • 카이제곱분포는 자유도 v의 크기에 따라 모양이 달라진다.
    • 자유도가 커질수록 분포가 좌우 대칭 형태로 된다.
    • 즉, 자유도가 커질수록 표준 정규 분포에 가까워진다.
      • $v \geq 30$이면 확률을 근사적으로 정규분포로 구할수 있다.

T 분포

  • $Z \sim N(0,1)$을 따르고, $Y \sim \chi^2$일때, $T = \frac{Z}{\sqrt{Y/v}}$를 따른다.

  • 확률변수 X가 정규분포를 따르고, 모표준편차 $\sigma$를 안다면
    • $z = \frac{X-\mu}{\sigma/n} \sim N(0,1)$

  • 만약 모표준편차 $\sigma$를 모른다면, $\sigma$를 대신해서 표본표준편차 s를 이용하여 확률변수 Z를 정의함

    • $t = \frac{X-\mu}{\sigma/n} \sim t(v)$

    • 여기서 $v$의 자유도는 n-1이다.

## F 분포

  • 서로 독립인 두 정규모집단의 분산 또는 표춘편차들의 비율에 대한 통계적 추론, 분산분석에 사용됨.

  • $Y_1 \sim \chi^2(v_2), Y_2 \sim \chi^2(v_2)$이면, $F \sim \frac{Y_1/v_1}{Y_2/v_2}, F \gt 0$

추정

추정

  • 모집단의 모수를 모를 경우 표본으로 추출된 통계량을 모집단의 근사값으로 사용하는것

  • 추정량

    • 표본 평균으로 모평균을 추정할 때, 표본평균을 모평균에 대한 추정량 이라고 한다.

  • 모수를 추정하는 방법에는 점 추정과 구간 추정이 있다.

    • 점 추정
      • 모수를 하나의 특정값으로 추정하는 방법
    • 구간 추정
      • 모수가 포함될 수 있는 구간을 추정하는 방법

점 추정의 성질

  • 일치성
    • 표본의 크기가 모집단의 크기에 근접해야 함.
    • 표본이 크기가 크면 클수록(모집단에 가까울수록) 추정량의 오차가 작아진다.
  • 불편성
    • 추정량이 모수와 같아야 함
    • 모수가 $\theta$이고, 추정량이 $\hat{\theta}$라고 정의하면, $E[\hat{\theta}] = \theta$이고, 이를 불편 추정량이라고 한다.
    • 즉, $E[\hat{\theta}] = \theta$일때의 추정량을 불편 추정량이라고 하고, 같지 않다면 편향(biased)되었다고 함
  • 유효성
    • 추정량의 분산이 최소값이어야 함
    • 모수에 대한 추정량의 분산이 작을수록 추정량이 효율적이다는 의미임.
    • 만약 모수 $\theta$의 불편 추정량이 $\hat{\theta_1},\hat{\theta_2}$라면 $Var[\hat{\theta_1}] \lt Var[\hat{\theta_2}]$이면, $\hat{\theta_1}$는 효율적인 추정량임
  • 평균오차제곱(MSE)
    • 평균오차제곱이 최소값이어야함
    • $E[(\hat{\theta}-\theta)^2]$이 최소여야 함.

구간 추정

  • 모수가 포함될 수 있는 구간을 추정하는 방법

  • 신뢰구간

    • 추정값이 존재하는 구간에 모수가 포함될 확률

    • 신뢰 수준은 $100 * (1-a)$% 로 계산하며, $a$는 오차 수준임

    • 신뢰 수준 95%라는것은 구간 추정된 값의 오차가 발생할 확률이 5%라는것을 의미함.

      • 이 오차를 유의 수준이라고 하며, p=0.05로 표현함
  • 신뢰구간은 신뢰 하한, 신뢰 상한으로 표시하며, 아래와 같은 수식으로 표현한다.

    • 이때, 추정하는 모수는 $\theta$이다.

    • $P[L(\hat{\theta} \le \theta \le U(\hat{\theta}))] = 1-a$

  • 만약 모평균$\mu$를 추정한다면, 표본평균이 $\overline{x}$이고 표준오차가 sd라고 하면 신뢰구간은 아래와 같다.

    • $\overline{x}-z \cdot sd \le \mu \le \overline{x}+z \cdot sd$

구간 추정에서 신뢰구간의 의미

모평균의 구간 추정

  • 모집단의 분산을 아는 경우

  • 모집단의 분산을 모르는 경우

    • T분포 사용

표본의 크기 결정

  • 허용 오차

    • 추정한 값이 틀려도 허용할수 있는 오차

    • 정규분포의 신뢰구간을 통해 허용 오차를 계산

    • $n = (\frac{z_{a/2}*\sigma}{d})^2$

모비율 추정

모비율의 점추정

  • 비율에 대한 추정

  • 우리가 원하는 속성에 속하면 1, 아니면 0일때, 1의 속성을 갖는 것의 개수를 X개라고 하면 $X~ B(n,p)$라고 한다.

  • 이때 모비율의 점추정량을 표본 비율이라고 함
    • $\hat{p} = (X / n)$

모비율의 구간 추정

  • 모비율 구간추정에서 정규분포의 근사가 가능한 대표본은 보통 $np \gt 5, n(1-p) \gt 5$를 동시에 만족해야함.

  • N이 충분히 크면 C.L.T에 의해서 $Z = \frac{\hat{p}-p}{\sqrt{p(1-p)/n}} \sim N(0,1)$

모평균 차이의 추정(점추정)

모평균 차이의 추정(구간추정 : 대표본)

모평균 차이의 추정(구간추정 : 소표본, 모분산 모를경우)

  • 두 모집단의 분산을 아는 경우에는 대표본과 동일하게 추정 가능하지만, 모르는 경우에는 등분산 가정이 필요하다.

  • 등분산 가정

    • 두 모집단의 분산이 같다는 가정

  • 합동 분산 추정량

    • 공통 분산의 추정량

    • T분포로 유도 가능

모비율 차이의 추정(점추정)

모비율 차이의 추정(구간추정)

You May Also Enjoy